大学受験のセンター試験では避けては通れなかった数1Aにある “論理と集合” 分野からの必要条件, 十分条件を努力にまつわる名言を使って解説してみる.
必要条件, 十分条件
赤い問題集(青い方が特に有名)の定義によれば,
命題 p ⇨ q が真であるとき,
q はp であるための 必要条件, p はq であるための十分条件という.
さて, 数学は抽象と具体を行き来する学問であるから早速具体例を見ていく.
努力した者が成功するとは限らない.
しかし, 成功する者は皆努力している.
引用文中の二行目にある「成功する者は皆努力している」に絞って話を進めていく.
ここで事象を”ある人に関して”次のように定める.
\begin{align}
p &: 成功する\\
q &: 努力する \\
\overline{p} &: 成功しない \\
\overline{q} &: 努力しない \\
\end{align}
上の表記に従い論理記号で書き換えると,
\begin{align}
p &\Rightarrow q は真\\
\end{align}
となる. 換言すれば「成功する者(p)は,皆努力をする者(q)だ」となる.
この命題が真ならば必要条件, 十分条件は次のように定義される.
努力(q)は成功(p)に対して必要条件
成功(p)は努力(q)に対して十分条件
前者は何かを成し遂げるためには, 努力は不可欠であること,
後者は, 努力に成功が伴えば努力していると言える. だが, 別に成功してなくとも努力している場合はある, だから成功は努力に対して過剰な条件となる,
といえば必要条件, 十分条件のイメージが湧くだろうか.
例題
上の議論を踏まえると必要条件, 十分条件を判断するための合言葉は次のようになる.
「成功する者(p)は皆努力している(q) 」は真であるから, p ⇨ q.
成功するには努力は必要だから, 努力(q)は成功(p)に対して必要条件.
したがって, p ⇨ q が真ならば, 十分 ⇨ 必要 (読み方は, 先が必要, 元が十分)
例題 次の()の中から適切な用語を選べ.
(1) x < 1 は x ≤ 1 であるための(必要条件, 十分条件, 必要十分条件).
(2) xy +1 = x + y は x, y のうち少なくとも1つは1であるための(必要条件, 十分条件, 必要十分条件)
(3) A < 90°は△ABCが鋭角三角形であるための(必要条件, 十分条件, 必要十分条件)
答え.
(1) p : x < 1 , q : x ≤ 1, と置けば, p ⇨ qは真.
合言葉より, 元が十分だから, 十分条件.
(2) p : xy + 1 = x + y, q : x, yのうち少なくとも1つは1, と置けば,
p : xy – x – y +1 = 0 ⇔ (x-1)(y-1) = 0 とかける. したがって p ⇔ qが真.
この場合は, 必要十分条件.
(3) p : A < 90°, q : △ABCが鋭角三角形 と置けば, q ⇨ pは真.
合言葉より, 先が必要だから, 必要条件.
注: 例題は pはqに対してどんな条件であるか, を問うていることに注意.
逆, 裏, 対偶で意味を深める
数学は思考の枠組みを提供してくれる. そこで, 逆, 裏, 対偶の意味を押さえるとともに, 逆, 裏, 対偶を通して上述の言葉の意味を深化させていく.
命題「p ⇨ q」 に対して, 逆,裏, 対偶は以下の画像のように定義される.
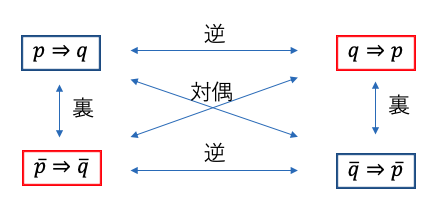
「p ⇨ q」 が真ならば, 対偶も真. しかし, 「p ⇨ q」 が真であっても,その逆や裏が真であるとは限らない.
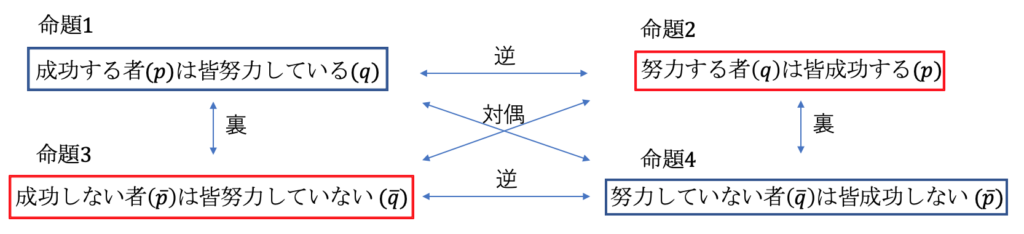
この事実を成功する者(p)は皆努力している(q) を用いて確認しよう. 画像を以下のように書き換える.
また, 最初に引用した文章をここで再掲しよう.
努力した者が成功するとは限らない.
しかし, 成功する者は皆努力している.
この言葉によると, 次のことが言える.
命題1「成功する者は皆努力している」は真である.
命題1の逆, 命題2「努力する者は皆成功する」は偽である.
対偶の特徴として, ある命題の真偽はその命題の対偶の真偽と等しいことが挙げられる. したがって, 対偶を取れば次のことが言える.
命題1の対偶, 命題4 「努力していない者は皆成功しない」は真である.
命題1の裏, 命題3「成功しない者は皆努力していない」は偽である.
これらの命題1~4から命題1の裏と逆が真偽が一致しないことが言葉の意味という観点から確認することができる.
今までの議論に沿うと引用文の一行目, 努力した者が成功するとは限らない, は 「q(努力する者)⇨ pの否定(成功するわけではない) 」は真 であることを意味している.
従って引用文について, それぞれの行の対偶を取り, 行の順番を入れ替えると(数学的には)全く同じ意味を含意する次の言葉を得ることができる.
努力しなければ成功しない.
しかし, 成功しない人は皆努力していないわけではない.
言葉の印象としては引用文は積極的な印象だがこの言葉は消極的な印象となった. 努力をしているけど成功せず, 落ち込んでいる人に向けて慰める言葉として使えるだろう.
まとめ
以上, 努力にまつわる言葉を用いて必要条件, 十分条件, 逆, 裏, 対偶の意味を解説した. 伝えたいこととして, 必要条件, 十分条件, 逆, 裏, 対偶の概念はただの数学的操作ではなく, 言葉の意味を正確に捉える手助けとなることである. わからない言葉や紛らわしい言葉があれば, その対偶を取れば意味が理解できる時がある.
———-雑感(`・ω・´)———-
対偶を用いれば意味が明確になる一例として次のような話がある.
脳の中にカオスが存在することを指摘した数学者に津田一郎先生がいる. 彼は自然科学の実験で得られる結論の表記が誤っていることがあることを指摘した上で実験の結果の解釈の仕方をインタビュー記事で簡単に説明していた.
よく行われる実験に次のようなものがある.
「あるマウスの遺伝子Aをノックアウトすると機能Bが働くなった.」
命題としてきちんと処理をすると結果の正確な解釈が明らかになる. 次のように事象p,qを定義する.
p : 遺伝子Aが存在する.
q : 機能Bが正常に働く
実験で明らかになることは 「pの否定 ⇨ qの否定」である. 対偶を取れば「q⇨ p」すなわち「機能Bが正常に働く⇨遺伝子Aが存在する」ことが正しいと言える. つまり, 遺伝子Aがあることは機能Bが正常に働くための, 必要条件である. 遺伝子Aは確かに機能Bの一部を担っているが機能Bは遺伝子A以外の要素によって定められている. ノックアウトマウスの実験は,機能Bに対する遺伝子Aの関与を示唆するがそれだけで機能Bの全貌を解明したとは決していうことができない. 度々ある過ちとしては「あるマウスの遺伝子Aをノックアウトすると機能Bが働くなった.」という結果を持って「遺伝子Aは機能Bを支配する」と言ってしまうこと, すなわち遺伝子Aを機能Bに対して必要十分条件であるかのように, 遺伝子Aと機能Bを一対一関係で完結するかのように解釈することは過ちである. 遺伝子Aは機能Bの一部分でしかないことを強調する.
———-雑感2(`・ω・´)———-
引用文と必要条件や十分条件, 対偶と結びつけて記事を書くヒントを与えてくれた武闘に石を使う人と山の中にある村に住んでいる住民に感謝だよ!
記事を書いていると, センター試験は平成で丁度終わりを迎え, 令和からは大学入試共通テストに移行することに気づいたよ. 世の中にとって”良い学力”を測定するようになることを祈るよ!
参考文献
・【努力は必ず報われるのか】これを読まずに努力をするな!偉人による努力の名言9選, https://atarimae.biz/archives/421


コメント