統計の勉強をしているとFishier’s information matrixとかHessianや複雑な関数の一回微分で数値微分が使えるという話はよくある.
また,数値微分をする際にはプログラムでの計算方法に付きまとう丸め誤差のせいで,小さすぎる値を用いてもダメという話もよくある.
じゃあ,どんな関数でどんな値を使って数値微分するべきなのか.
pythonのstatsmodelsのソースコードを見ている際に,数値微分に関する良い関数を見つけたので紹介したい.これで,一回微分もHessianも迷わずに求めることができるようになる.
数値微分の理論
以下の内容は,statsmodels.tools.numdiff と次の論文の内容を簡潔に書いたものである.”Ridout, M.S. (2009) Statistical applications of the complex-step method of numerical differentiation. The American Statistician, 63, 66-74″.
Θをスカラーだとすると,数値微分といえば良く出てくる式は以下の二つであろう.
$$
g_1(\theta) = \frac{f(\theta + \delta) – f(\theta)}{\delta} \\
g_2(\theta) = \frac{f(\theta + \delta) – f(\theta – \delta)}{2\delta}
$$
テイラー展開を用いることで以上の式は導ける.また,g1はO(δ), g2はO(δ^2)のオーダーで理論上は誤差を収めることができる.
statsmodelsの中ではさらにもう一つ,the Complex-Step methodという方法を用いていた.こちらの式もテイラー展開より示すことが可能.
$$
g_3(\theta) = \frac{ Im[ f(\theta + i\delta)]}{\delta}
$$
誤差は,O(δ^2)のオーダーとなる.しかし,このg3の方法を用いると丸め誤差をある程度避けることが出来るため実用上ではこちらが一番優秀な方法となる.
以下のコードは三つの数値微分の方法を比較したものである.関数 fはポアソン分布の対数の定数項を省いたもので,f(Θ) = y log(Θ) – Θ, で定義される.y=4,Θ=5のときf'(Θ) =-1/5 = -0.2 となる.
import numpy as np
from statsmodels.tools import numdiff
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set(context="paper" , style ="whitegrid",rc={"figure.facecolor":"white"})
def f(x):
y = x[0]
theta = x[1]
return( y*np.log(theta) - theta )
def fprime(x):
y = x[0]
theta = x[1]
return( y/theta- 1)
EPS = np.finfo(float).eps
logDelta = np.linspace(-17,0,100)
delta = np.power(10,logDelta)
dif1 = []
dif2 = []
dif3 = []
dif3m = []
x = np.array([4,5])
trueVal = fprime(x)
for e in delta:
d1 = numdiff.approx_fprime(x,f,epsilon=e,centered=False)
d2 = numdiff.approx_fprime(x,f,epsilon=e,centered=True)
d3 = numdiff.approx_fprime_cs(x,f,epsilon=e)
d1 = np.log10(np.abs(d1[1]-trueVal))
d2 = np.log10(np.abs(d2[1]-trueVal))
d3 = np.abs(d3[1]- trueVal)
d3m = np.clip(d3,EPS,np.inf)
d3 = np.log10(d3)
d3m = np.log10(d3m)
dif1.append(d1)
dif2.append(d2)
dif3.append(d3)
dif3m.append(d3m)
fig = plt.figure(figsize=(5,3),dpi=150)
ax = fig.add_subplot(111)
ax.plot(logDelta,dif1,label=r"g1($ theta $)")
ax.plot(logDelta,dif2,label=r"g2($ theta $)")
ax.plot(logDelta,dif3,label=r"g3($ theta $)")
ax.plot(logDelta,dif3m,label=r"g3($ theta $)",linestyle="dashed",color="green")
plt.legend()
plt.xlabel("$log_{10}(delta)$")
plt.ylabel("$log_{10}$(absolute error)")
plt.title("Absolute erros of the approximations")
plt.tight_layout()
plt.savefig("Absolute_erros_of_the_approximations.png")
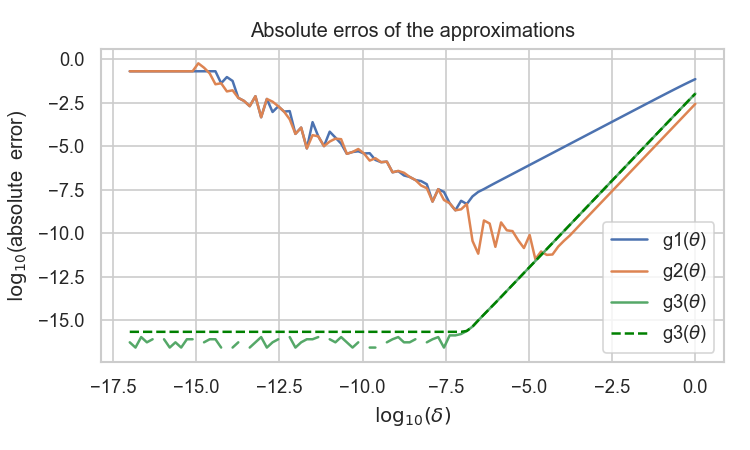
ただし,g3に関しては,Complex-Step methodによる差を表示する際には,丸め誤差で0になり対数を取る際にエラーが返ってくるのを防ぐために,EPS = np.finfo(float).eps (=2.220446049250313e-16, 僕のPCでの出力) で最小値を与えている点線も表示した.驚くことに,g1,g2の方法での数値微分で見られる与えるステップ幅が小さすぎて誤差が逆に大きくなってしまう問題が,Complex-Step methodでは見られない.
ソースコード
statsmodels.tools.numdiff のソースコードは,
import inspect import subprocess path = inspect.getfile(numdiff) subprocess.check_call(["open",path])
を用いて確認することができるが,コメントを抜いたversionを載せておく.approx_fprimeでg1,g2の実装,approx_fprime_csでg3の実装,approx_hess_csでhessianをComplex-Step methodで求める方法が書いてある.ちなみにこの方法は,論文の式(10)に該当する.
最小値の設定の仕方(EPS = np.MachAr().eps) やステップ幅の大きさの定め方など学ぶところは多かった.
EPS = np.MachAr().eps # np.finfo(float).eps と同じ.
def _get_epsilon(x, s, epsilon, n):
if epsilon is None:
h = EPS**(1. / s) * np.maximum(np.abs(x), 0.1)
else:
if np.isscalar(epsilon):
h = np.empty(n)
h.fill(epsilon)
else: # pragma : no cover
h = np.asarray(epsilon)
if h.shape != x.shape:
raise ValueError("If h is not a scalar it must have the same"
" shape as x.")
return h
def approx_fprime(x, f, epsilon=None, args=(), kwargs={}, centered=False):
n = len(x)
# TODO: add scaled stepsize
f0 = f(*((x,)+args), **kwargs)
dim = np.atleast_1d(f0).shape # it could be a scalar
grad = np.zeros((n,) + dim, np.promote_types(float, x.dtype))
ei = np.zeros((n,), float)
if not centered:
epsilon = _get_epsilon(x, 2, epsilon, n)
for k in range(n):
ei[k] = epsilon[k]
grad[k, :] = (f(*((x+ei,) + args), **kwargs) - f0)/epsilon[k]
ei[k] = 0.0
else:
epsilon = _get_epsilon(x, 3, epsilon, n) / 2.
for k in range(len(x)):
ei[k] = epsilon[k]
grad[k, :] = (f(*((x+ei,)+args), **kwargs) -
f(*((x-ei,)+args), **kwargs))/(2 * epsilon[k])
ei[k] = 0.0
return grad.squeeze().T
def approx_fprime_cs(x, f, epsilon=None, args=(), kwargs={}):
n = len(x)
epsilon = _get_epsilon(x, 1, epsilon, n)
increments = np.identity(n) * 1j * epsilon
partials = [f(x+ih, *args, **kwargs).imag / epsilon[i]
for i, ih in enumerate(increments)]
return np.array(partials).T
def approx_hess_cs(x, f, epsilon=None, args=(), kwargs={}):
n = len(x)
h = _get_epsilon(x, 3, epsilon, n)
ee = np.diag(h)
hess = np.outer(h, h)
n = len(x)
for i in range(n):
for j in range(i, n):
hess[i, j] = (f(*((x + 1j*ee[i, :] + ee[j, :],) + args), **kwargs)
- f(*((x + 1j*ee[i, :] - ee[j, :],)+args),
**kwargs)).imag/2./hess[i, j]
hess[j, i] = hess[i, j]
return hess
———-雑感(`・ω・´)———-
複素数での計算が定義されていない関数の評価を行うときだけ,approx_fprimeを使って,出来るだけapprox_frpime_csを使うようにすると,丸め誤差による微分値の正確性に対して不安にならなくて済む!


コメント