線形の重回帰分析をstatsmodelsのグラフ機能を出来るだけ使って行う

statsmodelsとは, scipyの統計の回帰関連で計算できる統計量が貧弱だったために新たに作られたmodule. それだけあって, 便利な機能が多い. 一度, 下記ページのTable of Contentsに目を通しておくと良い. 感動できる.

statsmodels statistitics in python, https://www.statsmodels.org/stable/index.html

ここでは, 重回帰分析をstatsmodelsを使って行う, 特にグラフ機能に焦点を当てて行なって回帰の妥当性の検証を行っていく.

準備
相関係数行列を確認する
線形モデルで多変量解析
statsmodelsのグラフ機能
1. 2変量間の関係を図示する
2. H Leverage と Outliers
終わり

準備

下記のコードをimport しておく. jupyter notebook上での動作を前提とする

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set(context="paper" , style ="whitegrid",rc={"figure.facecolor":"white"})

import statsmodels.api as sm
import matplotlib as mpl

また, データはstatsmodelsに入っているデータを使う.
だが, 実際の解析に近づけるために, pandasでデータをimportした時のように, 説明変数と結果変数が一つのデータフレームに存在するように加工する.

spectorData = sm.datasets.spector.load(as_pandas=True)
df = spectorData.exog
df["result"] = spectorData.endog
print(df.shape)
df.head().T

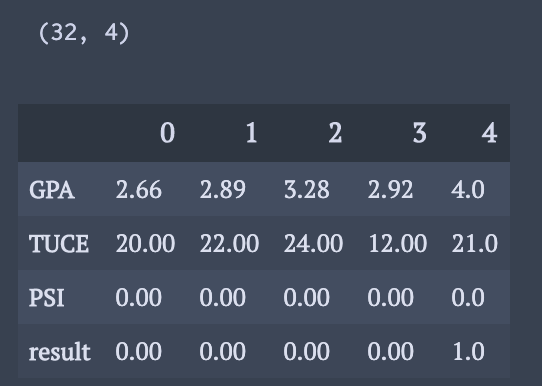
また, 切片用に”const”に1を格納.
説明変数と結果変数を表す変数を作っておく.

df["const"] = 1
expVar = ["GPA","TUCE","PSI","const"]
resVar = "result"

相関係数行列を確認する

多重共線性の問題を回避するために, 説明変数同士の相関係数はチェックしておく必要あり.
statsmodels のいくつかの描写機能は, fig = plt.figure(), ax = fig.add_subplot(111)で大きさが調整できないため, 一時的に図の大きさを変更する手段を取る.

import statsmodels.graphics.api as smg
df_ = df.copy().drop("const",axis=1)
corr_matrix = df_.corr()

with mpl.rc_context():
    mpl.rc("figure", figsize=(4,4),dpi = 100)
    smg.plot_corr(corr_matrix, xnames=df_.columns)

plt.show()

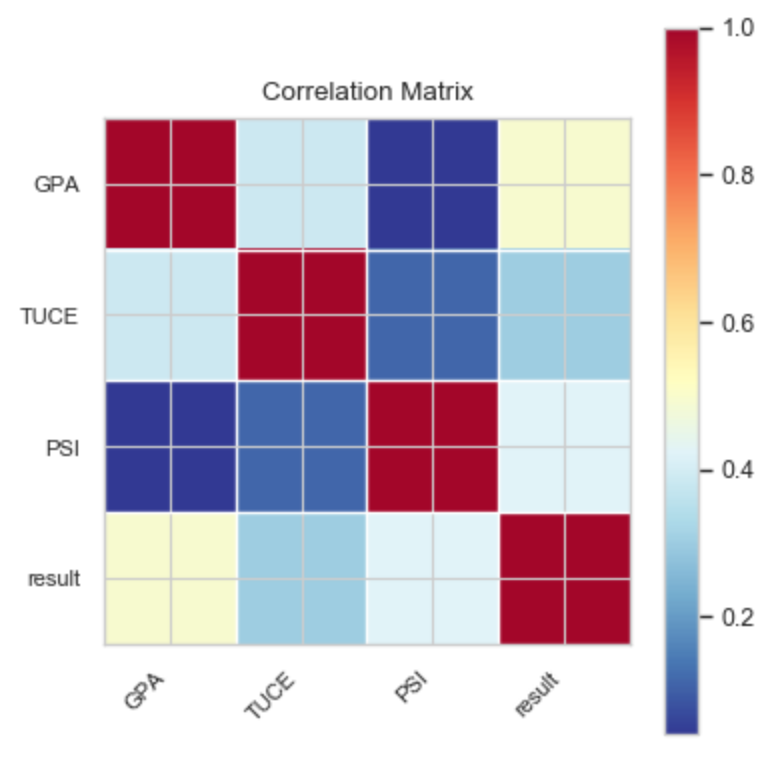
線形モデルで多変量解析

2行で結果を得られる.
推定値は最小二乗法により計算. (線形モデルだから X(‘X)-1X’Y で厳密解を計算しているのでしょう)
.summary()で結果を確認可能. 欲しい値がほぼあって嬉しい.

mod = sm.OLS(df[resVar],df[expVar])
res = mod.fit()
print(res.summary())

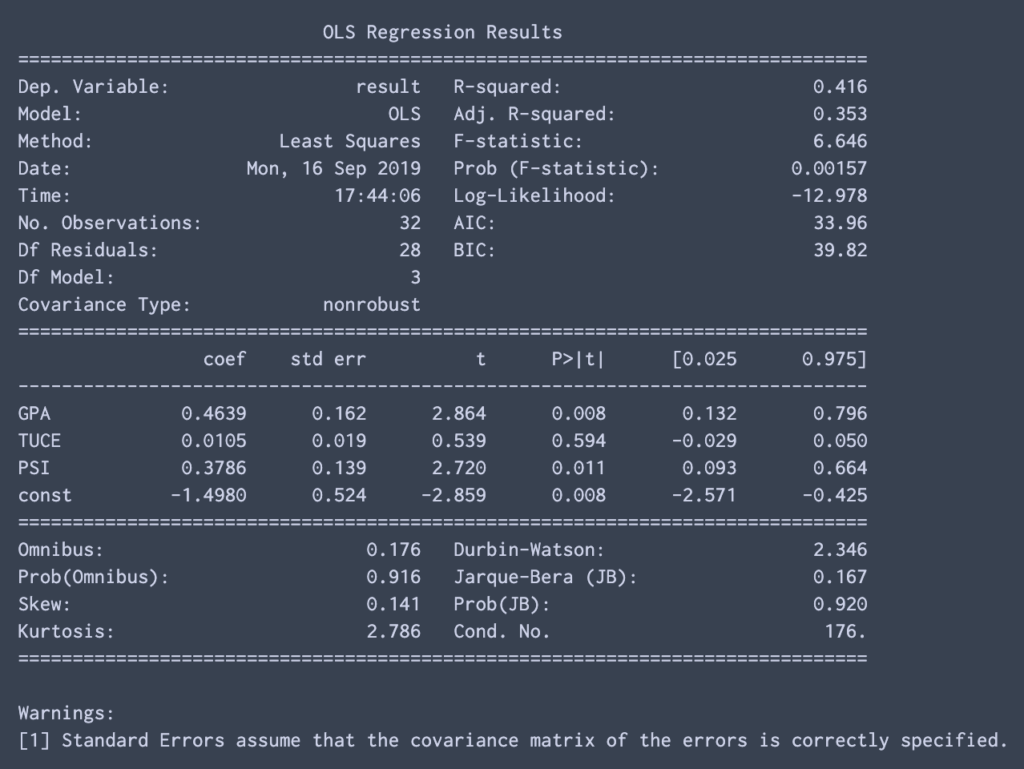
こういう新しいmoduleを用いるときに, どういうmethodが使えるか調べるのには, dir コマンドが便利. 今回の場合, dir(res) と打てば, 使えるmethodの名前一覧が表示される. 名前だけで大体何を示すか分かり, ググる手間が大幅に省ける.

上記の .summary()で表示した値のうち, 使いそうな値の抜き出し方を書いておく.

print("AIC : ", res.aic)
print("BIC : ", res.bic)
print("coefficients for each parameters : ",type(res.params))
print("----------------------")
print(res.params)
print("----------------------")
print("confidence interval for coefficients")
display(res.conf_int())
print("----------------------")
print("standard error for each coefficient")
print(res.bse)
print("----------------------")
print("fitterd values")
print(res.fittedvalues[:5])
print("----------------------")

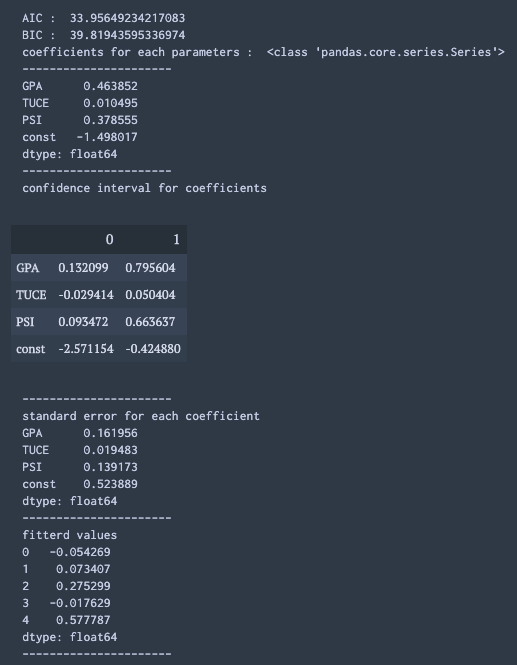
statsmodelsのグラフ機能

2変量間の関係を図示する

ここでは, 多変量解析の中である説明変数が結果変数をどれだけ説明しているか確認する方法を示す.

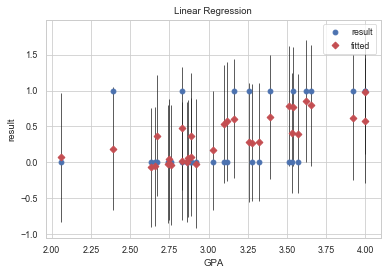
まずは, 単純に一つの説明変数と, 結果変数・推定値・信頼区間の図示.
ここでは, 多変量で回帰を行なっているので直線関係がみえないことに注意. また, ここで相関関係が一切無いようにみえても, 他の説明変数で調整を行うとしっかりとした相関がみられることがあるので注意.

target = "GPA"
fig, ax = plt.subplots()
fig = sm.graphics.plot_fit(res, target, ax=ax)
ax.set_title("Linear Regression")

次の機能は図ごとに解説が必要.
まずは, コードと機能と写真の掲載.

fig = plt.figure(figsize=(8,6),dpi = 100)
sm.graphics.plot_regress_exog(res, 'GPA', fig=fig)
plt.show()

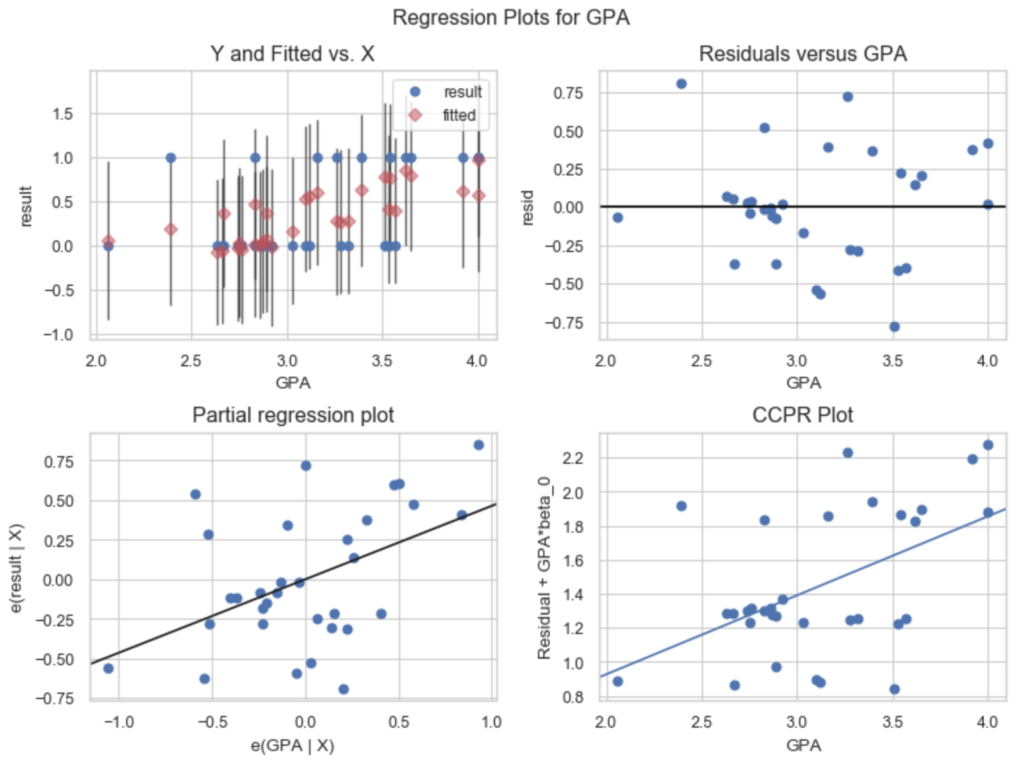
これは, 説明変数”GPA”がどれだけ”result”の変数を説明しているかについて観察する4つの図である.

左上のグラフは, 一つ前と同じで, 説明変数と結果変数・推定値・信頼区間を図示している. これによって推定値が実際の値をどれだけ予測できているかを表している.

右上のグラフは, 説明変数に対する結果変数との残差(Residual)を表している. 丁度左上の図の青点の値から赤点の値を引いた値がy軸にplotされていることが分かる.

左下の図は, Partial Regression Plot. x軸に, “GPA”以外の変数を用いて,”GPA”を回帰した時の残差を用いる. y軸に”GPA”以外の変数を用いて”result”を回帰した時の残差を用いる. こうすることで, 他の変数を調整した時の変数間の関係をみていることになる.
厳密ではないが, 下の資料の”What multiple regression coefficients mean”の項が分かりやすかった.

UC_berkeley_statistics_29_multi ダウンロード

右下のCCPR(component and component-plus-residual) plotは, 左下のグラフに, x軸には”GPA”の値を足して, y軸には (全モデル推定して得られた係数)*(“GPA”の値)を足したものである. もし, “GPA”が”result”を良く説明しているのならば, 点は直線の上に集まるはずである. ただし, 変数間に相関関係が強くある場合にはこの限りではないため, 解釈には注意が必要である.

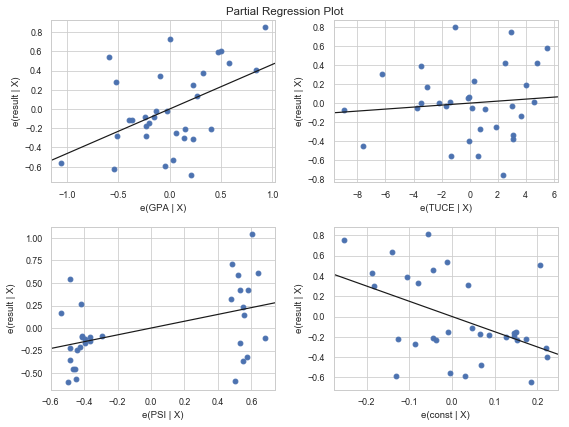
全ての説明変数に対して, 一気にPartial Regression Plot, CCPR plotを行うことも可能である.
ここでは, Partial Regression Plotのコードと図を載せておく.

from statsmodels.graphics.regressionplots import plot_partregress_grid
fig = plt.figure(figsize=(8,6))
plot_partregress_grid(res, fig=fig)
plt.show()

H Leverage と Outliers

Outliers は外れ値を意味し, 異常な値を持っている結果変数をいう.
一方, H Leverage は, 異常な値, もしくは異常な値の組みを持つ説明変数を見つけるための指標だ.
Outliers をみつけるのは簡単. 結果変数だけに関してhistgramやboxplotを描いてあげればいい.
だが, 異常な組を持つ説明変数を見つけるのは容易ではない. 例えば, どの変数の値も正常な範囲に収まっているが, 組としてみたときにあり得ない値の組であることは往々にしてありうる.

数式的な説明は, Google Sheets の解説が分かりやすかった.

さて, このH Leverageをplotするcodeがこちら.

from statsmodels.graphics.regressionplots import plot_partregress_grid

with mpl.rc_context():
    mpl.rc("figure", figsize=(4,4),dpi = 100)
    sm.graphics.influence_plot(res)
    cutOff = 2*(res.df_model + 1)/res.nobs
    plt.axvline(x = cutOff,color="r",alpha=0.5)
    plt.show()

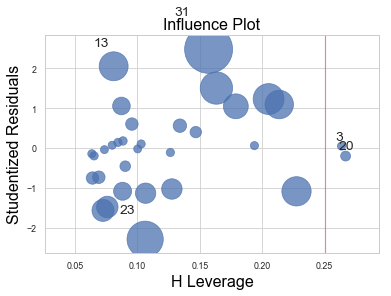
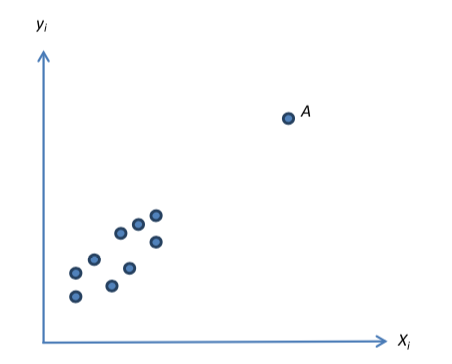
x軸に先ほどまで説明していたH Leverageという指標が使われている.
cut-off値としては, 2*(切片も含めたパラメータの数)/(データ数) が挙げられる.
すると, 上図での3,20番目のデータは異常値なのだろうか？ H Leverageは, 結果変数を用いない説明変数内での相似性から離れた点を見つける指標である. だから, 以下のような回帰直線には載るが他の点から離れているものもH Leverageの値が大きくなってしまう. だから, ここでもう一つ, どれだけ回帰直線から離れているかという指標も用いなければいけない. 上図のStudentized Residualsはその指標の一つだ. この二つを勘案して影響が大きい点のバブルのサイズを変えて図示したのが, 上図のInfluence Plotの正体となる.

Studentized Residualsの代わりにNormalized residuals**2 を用いた図が下である.

from statsmodels.graphics.regressionplots import plot_partregress_grid
with mpl.rc_context():
    mpl.rc("figure", figsize=(8,8),dpi = 100)
    sm.graphics.plot_leverage_resid2(res)
    cutOff = 2*(res.df_model + 1)/res.nobs
    plt.axhline(y = cutOff,color="r",alpha=0.5)
    plt.show()

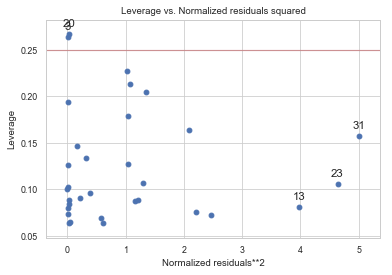
終わり

以上, pythonのstatsmodelsを用いて多変量線形回帰モデルの実装とその解釈をするためのグラフについて書いた.

———–雑感(｀・ω・´)———-
ちょうどstatsmodelsのように回帰の変数の信頼区間を自動で計算するコードを書かなければいけないのか！？と考えていたところだから助かった…
研究的には, 相関係数行列の値の大小とその相関係数が有意に存在するかは別の話だから, 変数間の依存関係に注意して, 一つの説明変数と結果変数間で相関関係が有意に存在するかの検定を行うことには価値があると思う.