scipy.minimizeをすっきり書く書き方 | あきとしのスクラップノート

この記事では，scipy.minimizeを効率的に運用していく方法を書く．特にニュートン共役勾配法など勾配ベクトル・ヘシアンが必要になる最適化手法を用いる時に有効な手段である．

結論から言えば，クラスを用いて評価関数，勾配ベクトル，ヘシアンを書き，それをラッパー関数で覆ってscipy.minimizeにクラスごと渡す方法を取る．

コードは，git clone https://github.com/akitoshiblog/blogsiteでminimize_simpleの下にある.

以下は関係する記事．
・非線形最適化関数scipy.minimizeの各手法の実装例
・[python] Logistic Regressionを用いてOdds Ratioを求める

下準備・理論
クラスの準備
scipy.minimizeで推定
おまけ

下準備・理論

以下のmoduleをimportする．

import pandas as pd
import numpy as np
from scipy.optimize import minimize
import statsmodels.api as sm

クラスの準備

ここでは例として，Logistic Regressionを取り上げる．
内生変数として 0 or 1 を取る t ( N ベクトル) , 外生変数としてX (N*M行列)と表し，切片ベクトルを w (Mベクトル)とする．

リンク関数としてlogit関数，尤度関数に対しては二項分布を選ぶので尤度関数は以下のように表される．

$$
y_i = frac{ 1}{1+ exp(wX_i)} \
L = prod_i^N y_i^{t_i} (1-y_i)^{1-t_i}
$$

ここでXi はXのn列目，n番目の入力を表す．
従って，negative log likelihood(nll), その勾配ベクトル(g)，ヘシアン(h)は次のように表される．

$$
nll = -sum t_i log y_i + (1-t_i) log(1-y_i) \
g = nabla_w nll = X (y-t)\
h = nabla_w nabla_w nll = X^T R X
$$

ここでRはRii = yi(1-yi) で与えられる対角行列である．

これらを計算するコードと，後述するsetParams, initParamsをメソッドとして持ったクラスを記述する．

EPS = np.finfo(float).eps
def logiFunc(x):
    v = 1./(1. + np.exp(-x) )
    v = np.clip(v,EPS,1-EPS)
    return(v)

class logisticRegression():
    def __init__(self,endog,exog):
        self.M = len(exog[0])
        self.N = len(exog)
        
        self.X = np.array(exog)
        self.t = np.array(endog)

    def pred(self):
        linear = (self.w * self.X).sum(axis=1) 
        self.y =  logiFunc(linear)   

    def logLikelihood(self):
        self.pred()
        t = self.t
        y = self.y
        ll = t * np.log(y) + (1-t)*np.log(1-y) 
        ll = ll.sum()
        return(ll)

    def grad(self):
        g = self.X.T @ (self.y- self.t)
        return(g)

    def hess(self):
        R = self.y*(1-self.y)* np.eye(self.N) 
        H = self.X.T @ R @ self.X
        return(H)
    
    def setParams(self,x):
        self.w = x 
    
    def initParams(self):
        # initial values for w
        x = np.zeros(shape=(self.M))
        return(x)

次にこのクラスにデータをセットする．データはstatsmodelsのサンプルデータを用いる．変数の選択は適当．

df = sm.datasets.anes96.load_pandas().data
exog = ["TVnews","selfLR","PID","educ"]
endog = "vote"
evalF = logisticRegression(df[endog].values,df[exog].values)

scipy.minimizeで推定

上のクラスの定義でのポイントは
・一度データをセットすれば，パラメータを更新する度に，log likelihood, 勾配ベクトル，ヘシアンを次々に計算出来るようにしている点
・ setParamsは一つのパラメーターが与えられた時にクラスで用いる変数の形に分解して引き渡す．今回は，wにそのまま代入するだけなのでシンプル．
・initParamsは初期値の生成に用いる．

このようにクラスを準備した後，以下のWrapper関数を用意すれば，下のコードは一行も変えずに推定することが可能となる．

def fWrapper(x,evalF):
    evalF.setParams(x)
    nll = -evalF.logLikelihood()
    print(nll)
    return(nll)

def gradWrapper(x,evalF):
    g = evalF.grad()
    return(g)

def hessWrapper(x,evalF):
    h = evalF.hess()
    return(h)

x0 = evalF.initParams() 
result = minimize(fun = fWrapper,
                  x0=x0, 
                  args = (evalF,),
                  jac= gradWrapper,
                  hess = hessWrapper,
                  method="Newton-CG")
print(result)

　ただし，以上のコードは，”Newton-CG”の場合，関数が呼び出される順番がfun -> jac -> hessであることを踏まえて書かれていることに留意すること．

　以上の書き方をすることで，fun, jac, hessのために別々に関数を書かずに一貫したコード作成が可能となる．

おまけ

今回はおまけで，パラメータの信頼区間をObserved Fisher Informationを用いて求める．それは，推定された値を用いてヘシアンの逆行列の対角要素のルートを各パラメータの標準偏差とする．

def calConf(res,evalF):
    evalF.setParams(res.x)
    evalF.logLikelihood()
    h = evalF.hess()
    hInv = np.linalg.inv(h) 
    sd= np.sqrt(np.diag(hInv))
    return(sd)

def dispRes(exogNames,res,sd):
    l = [len(x) for x in exogNames]
    maxL = np.max(l)
    n =  10
    nLine = maxL + 45

    s = ("{:^%d}n"% nLine).format("Logistic Regression Results") +
        "="*nLine +   "n" +
       ("{: <%d}  {: >%d} {: >%d} {: >%d} {: >%d}n"% (maxL,n,n,n,n))
                .format("","coef","std err","[0.025","0.975]") +
        "-"*nLine +   "n" 
    for name, x,c in zip(exogNames,res.x,sd):
        s += ("{: <%d}  {: >%d.4f} {: >%d.3f} {: >%d.3f} {: >%d.3f}n"
                % (maxL,n,n,n,n)).format(name,x,c,x-c*1.96,x+c*1.96)
    s +=  "="*nLine +   "n" 
    print(s)


sd = calConf(result,evalF)
dispRes(exog,result,sd)

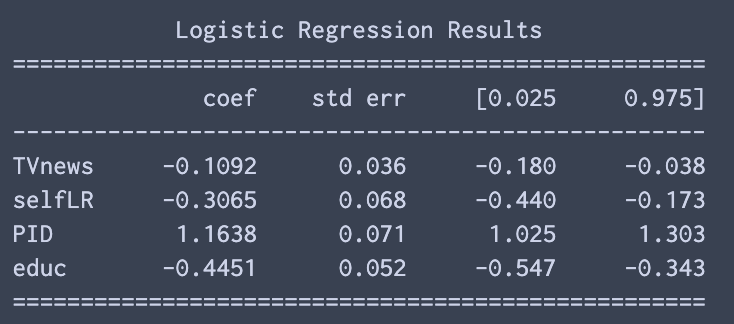
これが正しいかどうか，statsmodelsの結果と比較する．

mod = sm.GLM(df[endog],
             df[exog],
             family=sm.families.Binomial())
res = mod.fit()
print(res.summary())

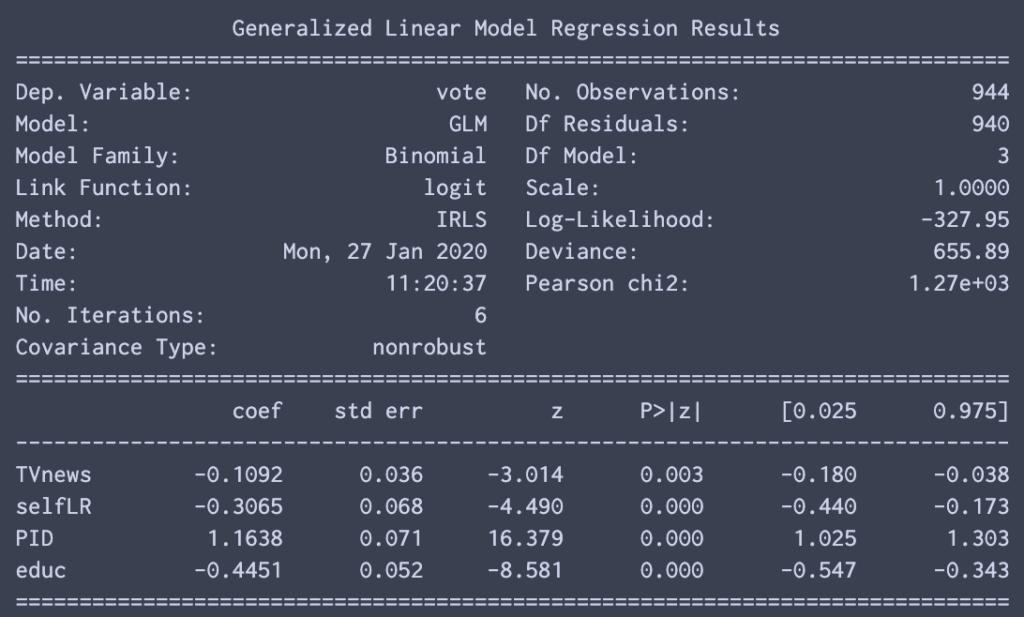
ほぼ同じ結果が得られたので安心です．