非線形最適化関数scipy.minimizeの各手法の実装例 | あきとしのスクラップノート

この記事では，非線形関数の最適化問題を解く際に用いられるscipy.optimize.minimizeの実装を紹介する．minimizeでは，最適化のための手法が11個提供されている．ここでは，[1]の分類に従って実装方法を紹介していく．

分類

非線形関数の最適化問題を解く手法では，勾配ベクトル・ヘシアンの要，不要とパラメーターに制約が掛かるかどうかで手法の選択が分かれる．

1.非制約最適化問題．
1.1. 勾配ベクトル・ヘシアンが不要．
・ Nelder-Mead法
・ Powell法
1.2. 勾配ベクトルが必要．
・共役勾配法 (conjugate gradient method),
・BFGS法 (Broyden–Fletcher–Goldfarb–Shanno method)
1.3. 勾配ベクトル・ヘシアンが必要．
・ニュートン共役勾配法 (Newton conjugate gradient method)
・信頼領域ニュートン共役勾配法 (Newton conjugate gradient trust-region method)
・信頼領域dog-leg法 (dog-leg trust-region method)

2. 制約付き最適化問題
COBYLA法以外，勾配ベクトルが必要な手法．
2.1. パラメーターの範囲に制限がある場合．
・範囲制約付きメモリ制限BFGS法(L-BFGS-B)
・切断ニュートン共役勾配法(TNC)
2.2. 等式・不等式制約がある場合．
・COBYLA法 *(constrained optimization by linear approximation method)
・sequential least squares programming (SLSQP)
*不等式制約のみサポート

準備

実装のために，以下のmoduleをimportしておく．

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set(context="paper" , style ="whitegrid",rc={"figure.facecolor":"white"})

from scipy.optimize import minimize

import matplotlib.patches as mpatches
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm

非線形関数としてはRosenbrock’s banana function[3]を用いる．scipy.optimizeの中にも関数は実装されているがargsの使い方も例示出来るように改めて自分で定義する．また，Rosenbrock’s banana functionの勾配ベクトルとヘシアンも定義しておく．

def f(x,args ):
    v = (args[0] - x[0])**2 + args[1]*(x[1] - x[0]**2)**2
    return(v)

def grad(x,args):
    delx = 2*(x[0]- args[0]) + 4*args[1]*x[0]*(x[0]**2 - x[1])
    dely = 2*args[1]*(x[1] - x[0]**2)
    g = np.array([delx,dely])
    return(g)

def hess(x,args):
    delxx = 2 + 12*args[1]*x[0]**2 - 4*args[1]*x[1]
    delxy = -4*args[1]*x[0]
    delyx = delxy
    delyy = 2*args[1]
    h = np.array([[delxx,delyx],[delxy,delyy]])
    return(h)

args = (1,100)
x0 = [2,2]

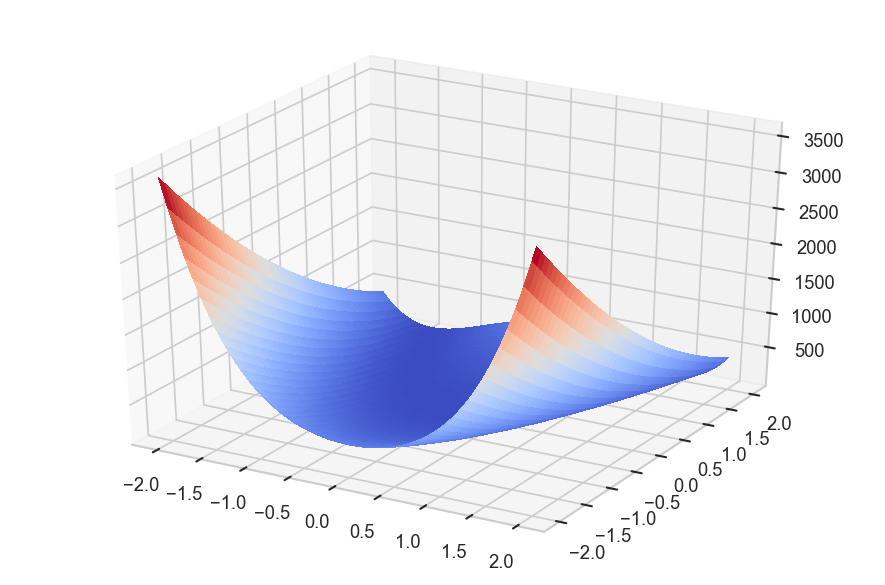
ちなみにRosenbrock’s banana functionは次の式で与えられ，大域最小解は，(x,y) = (a,a) である．

$$
f(x,y) = (a-x)^2 + b(y-x^2)^2
$$

x = np.linspace(-2,2,100)
y = np.linspace(-2,2,100)
xx,yy = np.meshgrid(x,y)
zz = f([xx,yy],args)
fig = plt.figure(figsize=(6,4),dpi=150)
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(xx,yy,zz,cmap=cm.coolwarm,linewidth=0, antialiased=False)
plt.tight_layout()

非制約最適化問題．

勾配ベクトル・ヘシアンが不要．

Nelder-Mead法

minimizeの一番の基本形．

result = minimize(fun = f,
                  x0=x0, 
                  args = (args,),
                  method="Nelder-Mead")
print(result)

tolで推定の際の制度を指定できるが方法によってtolの扱いが変化する．また，optionで方法ごとに細かいパラメーターの調整とdispで推定が成功したかどうかを表示することが可能．

result = minimize(fun = f,
                  x0=x0, 
                  args = (args,),
                  method="Nelder-Mead",
                  tol = 1e-1,
                  options={"disp":True})

Powell法

result = minimize(fun = f,
                  x0=x0, 
                  args = (args,),
                  method="Powell")
print(result)

勾配ベクトルが必要．

共役勾配法 (conjugate gradient method)

勾配ベクトルをjacに引き渡す．

result = minimize(fun = f,
                  x0=x0, 
                  args = (args,),
                  jac= grad,
                  method="CG")
print(result)

勾配ベクトルを指定しないことも出来る．その場合は，数値微分によってjacobianが評価される．jac=False にしなくとも，jacを渡さなければ数値微分によってjacobianが評価される．当然だが，jacobianを渡した方が推定の精度は良い．

result = minimize(fun = f,
                  x0=x0, 
                  args = (args,),
                  jac=False,
                  method="CG")
print(result)

BFGS法 (Broyden–Fletcher–Goldfarb–Shanno method)

result = minimize(fun = f,
                  x0=x0, 
                  args = (args,),
                  jac= grad,
                  method="BFGS")
print(result)

勾配ベクトル・ヘシアンが必要．

ニュートン共役勾配法 (Newton conjugate gradient method)

jacに勾配ベクトル, hessにヘシアンを渡す．

result = minimize(fun = f,
                  x0=x0, 
                  args = (args,),
                  jac= grad,
                  hess = hess,
                  method="Newton-CG")
print(result)

最低限，勾配ベクトルは渡す必要あり．勾配ベクトルから数値微分によってヘシアンが評価される．

result = minimize(fun = f,
                  x0=x0, 
                  args = (args,),
                  jac = grad,
                  method="Newton-CG")
print(result)

信頼領域ニュートン共役勾配法 (Newton conjugate gradient trust-region method)

あとは，方法の引数変えるだけで実装可能です．

result = minimize(fun = f,
                  x0=x0, 
                  args = (args,),
                  jac= grad,
                  hess = hess,
                  method="trust-ncg")
print(result)

信頼領域dog-leg法 (dog-leg trust-region method)

result = minimize(fun = f,
                  x0=x0, 
                  args = (args,),
                  jac= grad,
                  hess = hess,
                  method="dogleg")
print(result)

2. 制約付き最適化問題

パラメーターの範囲に制限がある場合．

範囲制約付きメモリ制限BFGS法(L-BFGS-B)

パラメーターの範囲をboundsにtupleで引き渡す．もし大量のパラメーターに同じ制約を付けさせたければ，((2,None),)*20 のようにすればよい．片側だけに制限を付ける場合は，Noneかnp.infを用いる．

result = minimize(fun = f,
                  x0=x0, 
                  args = (args,),
                  jac= grad,
                  bounds = ((2,None),(2,np.inf)),
                  method="L-BFGS-B")
print(result)

切断ニュートン共役勾配法(TNC)

result = minimize(fun = f,
                  x0=x0, 
                  args = (args,),
                  jac= grad,
                  bounds = ((2,None),) *2,
                  method="TNC")
print(result)

等式・不等式制約がある場合．

COBYLA法 (constrained optimization by linear approximation method)

勾配ベクトル・ヘシアンが不要な方法．COBYLA法は不等式制約のみを受け付ける．boundsも使えない．以下のように制約を与えるが，条件は "type":"ineq" にすると関数が非負にならないように調整する．つまり，x[0]-2 は　x[0]-2 >= 0 になるように制限される．

cons = ({"type":"ineq","fun": lambda x: x[0] -2},
       {"type":"ineq","fun":lambda x:x[1] - 5 })
result = minimize(fun = f,
                  x0=x0, 
                  args = (args,),
                  constraints= cons,
                  method="COBYLA")
print(result)

sequential least squares programming (SLSQP)

boundsも等式制約もつけられる手法．

cons = ({"type":"ineq","fun": lambda x: x[0] - 2},
       {"type":"eq","fun":lambda x:x[1] - x[0] })
result = minimize(fun = f,
                  x0=x0, 
                  args = (args,),
                  jac= grad,
                  bounds = ((-1,None),) *2,
                  constraints= cons,
                  method="SLSQP")
print(result)

———-雑感(｀・ω・´)———-
各手法に対して何を引数として与えるか，どうやって与えるか，整理出来て良かったです．