この記事では, pythonのscikit-learnで提供されている混合ガウスモデル(Gaussian Mixture Model, GMM)を用いたクラスタリングの実装について解説する.
目標としては, scikit-learnの公式ドキュメントにある図をirisのデータセットに対して置き換える. そして図の下をPCA(Principal Component Analysis)を用いて, クラス分けの結果を可視化した図にすることである.
scikit-learnのオプションについて
始めに, 混合ガウス分布を利用するにあたってモデルの簡単な説明とscikit-learnのオプションの設定の意味を概説する.
混合ガウス分布モデルは, 次の式によって表現される.
$$ p(x) = \sum_{k=1}^{K} \pi_k N(x|\mu_k,\Sigma_k) $$
ここで, Kはクラスターの総数を示している. クラスの分け方としては, 各kに関してΣの中身が最大, つまりπ*Nが最大となるようなものにクラスを割り振ることとなる.
scikit learnで実装されている混合ガウス分布によるクラスタリングでは, π, μ, ΣをEM algorithmを用いて推定している. 理論については, を参照のこと.
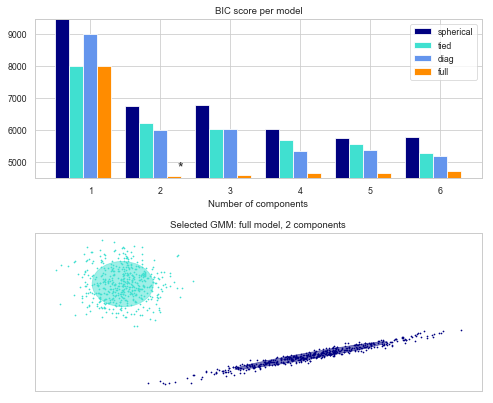
をみると, irisのデータセットに関してGMMを用いた結果が表示されている. x軸, y軸はそれぞれ, “sepal length (cm)”, “sepal width (cm)”である.
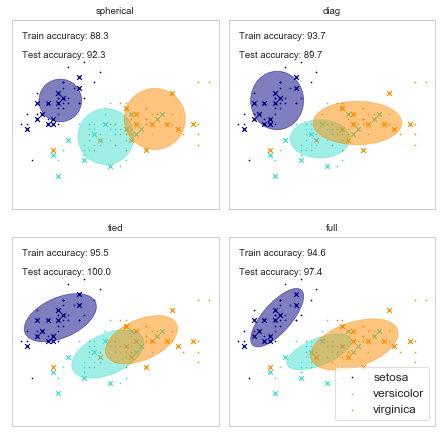
ここで, 4つのtype, “spherical” ,”diag”, “tied”, “full” の4つの設定がある. 公式ドキュメントには次のように載っている.

“spherical”の場合は, 一つのクラスターに関して, 分散は一つしかない, つまりモデルは次のように表される.
$$ p(x) = \sum_{k=1}^{K} \pi_k N(x|\mu_k, \alpha_k^ I) $$
“diag”の場合は, 各クラスターに関して, 対角要素の分散が与えられる. つまり,
$$ p(x) = \sum_{k=1}^{K} \pi_k N(x|\mu_k,\Sigma_k) $$
において, データxの次元が3次元だとすると,
$$
\Sigma_k =
\begin{pmatrix}
\sigma_{k11} & 0 & 0 \\
0 & \sigma_{k22} & 0 \\
0 & 0 & \sigma_{k33}
\end{pmatrix}
$$
で与えられる.
“tied” は, クラスターに関わらず同じ分散共分散行列を持つことを述べている. 数式としては以下のように与えられる. 分散共分散行列から添字のkがなくなっていることに注意. 実際は, ガウス分布の制約から分散共分散行列は対称行列となる.
$$ p(x) = \sum_{k=1}^{K} \pi_k N(x|\mu_k,\Sigma) $$
“full”は制限なしのモデルである.
準備
実装に移っていく.
以下のモジュールをインポートしておく. 実行はjupyter notebook上を想定.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set(context="paper" , style ="whitegrid",rc={"figure.facecolor":"white"})
from scipy import linalg
import itertools
# for Gaussian Mixture model for classification
from sklearn import mixture
# for PCA (principal component analysis)
from sklearn.decomposition import PCA
# for sample data
from sklearn import datasets
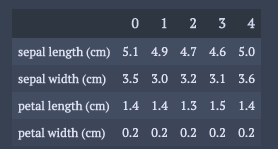
また, irisのデータセットを構造化されたデータと同じように加工しておく.
dataset = datasets.load_iris()
dic = {}
for k,v in zip(dataset.feature_names,dataset.data.T):
dic[k] = v
df = pd.DataFrame(dic)
df.head().T
GMMの実装と可視化
実装内容は, ほぼ参考. データの入力の仕方と変数の名前の付け方, fittingの際の初期値を変えての実行回数(defaultだと1回)を10回に設定しているところだけが相違点. 何回も初期値を変えて実行しているのは, EM algorithmにおいては最適解にいかない場合があるから. これは, GMM自体が設定不良問題になってしまっているから. 詳細はのCh.9参照.
X = df.values
lowestBIC = np.infty
bic = []
nComponentsRange = range(1, 7)
cvTypes = ['spherical', 'tied', 'diag', 'full']
nInit = 10
for cvType in cvTypes:
for nComponents in nComponentsRange:
# Fit a Gaussian mixture with EM
gmm = mixture.GaussianMixture(n_components=nComponents,
covariance_type=cvType,n_init =nInit)
gmm.fit(X)
bic.append(gmm.bic(X))
if bic[-1] < lowestBIC:
lowestBIC = bic[-1]
bestGmm = gmm
bic = np.array(bic)
colorIter = itertools.cycle(['navy', 'turquoise', 'cornflowerblue',
'darkorange'])
bars = []
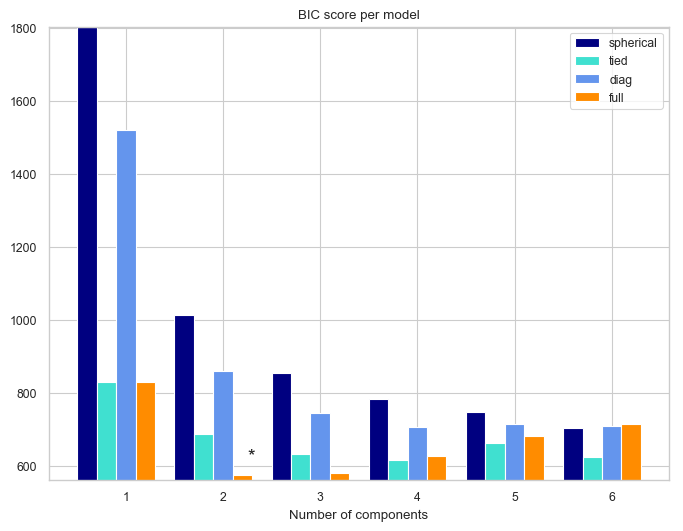
# Plot the BIC scores
plt.figure(figsize=(8, 6),dpi=100)
ax = plt.subplot(111)
for i, (cvType, color) in enumerate(zip(cvTypes, colorIter)):
xpos = np.array(nComponentsRange) + .2 * (i - 2)
bars.append(plt.bar(xpos, bic[i * len(nComponentsRange):
(i + 1) * len(nComponentsRange)],
width=.2, color=color))
plt.xticks(nComponentsRange)
plt.ylim([bic.min() * 1.01 - .01 * bic.max(), bic.max()])
plt.title('BIC score per model')
xpos = np.mod(bic.argmin(), len(nComponentsRange)) + .65 +
.2 * np.floor(bic.argmin() / len(nComponentsRange))
plt.text(xpos, bic.min() * 0.97 + .03 * bic.max(), '*', fontsize=14)
ax.set_xlabel('Number of components')
ax.legend([b[0] for b in bars], cvTypes)
可視化に関しては, 以前の記事( pythonでk means clusteringの結果をPCAを用いて2次元と3次元で確認する ) に載っている関数を用いて行う. 関数部分のコードは省略した.
varNames = df.columns # normalization dfScaled = df.copy()[varNames] dfScaled = (dfScaled - dfScaled.mean())/dfScaled.std() # principal components analysis pca = PCA(n_components=3) trans= pca.fit_transform(dfScaled[varNames]) # insert results of GMM clustring dfScaled["clusterId"] = bestGmm.predict(X) # these functions are defined in the previous article. summaryPCA(pca,varNames) contriPCAPlot(pca,varNames) clusterPCAPlot(trans,dfScaled)
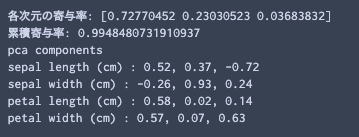
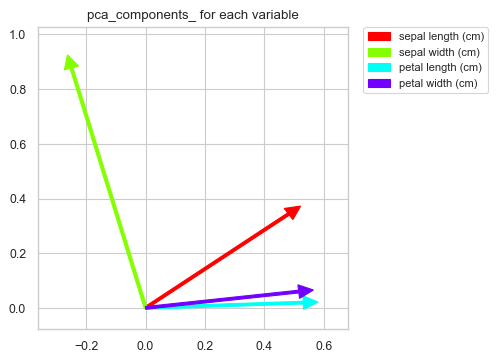
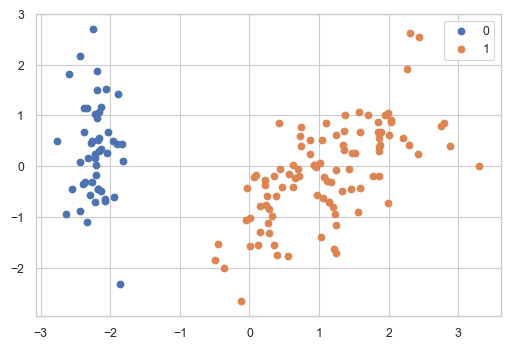
結果の解釈について
iris datasetはもともと, "setosa", "versicolor", "virginica"の3種から構成されたデータセットであったが, BICに基づいた分類では次数が2の"full"モデルが最も良いと判断された. これはモデルの適合度(goodness of fit)を表す指標が, 現実を正確に表すわけではない例といえる.
以下の画像はscikit-learnが出している, 解析の際にどのalgorithmを使えば良いかに関してのcheat-sheetである.
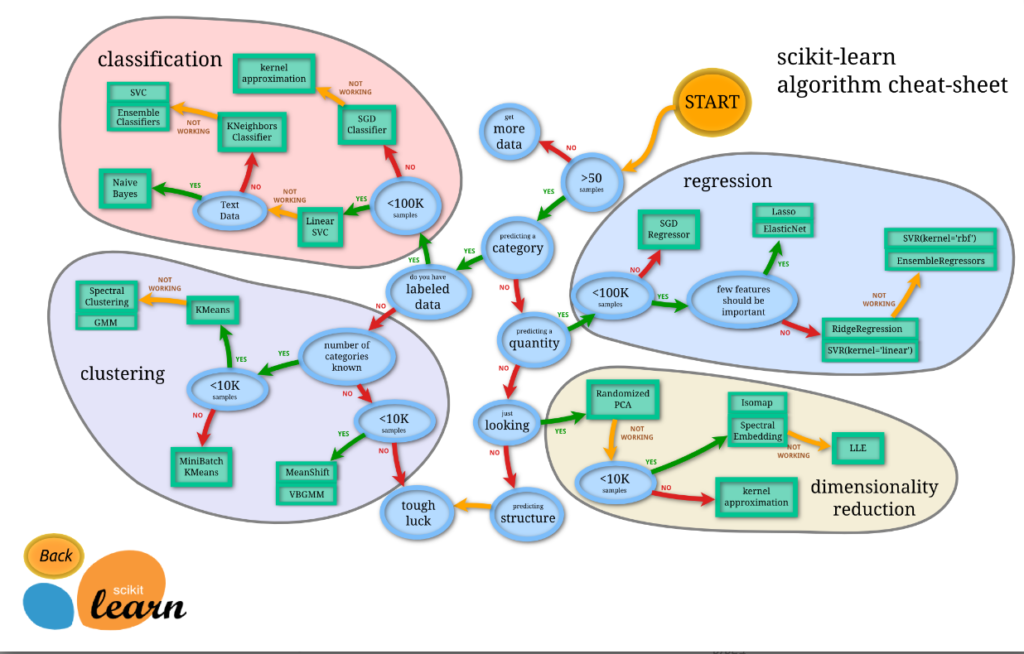
このcheet-sheetに従えば, クラスタリングがカテゴリーでクラスターの数が決まっていない場合は, "MeanShift"か"VBGMM"を用いることが推奨されている. しかし, どちらの方法もクラスターの数を定めなくても良い代わりに, hyper parameterの調整が必要になってくる. だが, そのhyper parameterを選ぶのは恣意的な作業で交差検定の作業が必要になってくる. 個人的には, それをやるくらいならば, 今回のように次数ごとにBICを計算して, 最もBICが良かったクラスターの数を採用するのが楽なように思える.
----------雑感(`・ω・´)----------
先のような議論は, reversible jump MCMCを使った時に感じたことである. reversible jump MCMCは, モデル間の推移も含めてパラメーターを推定しようという方法なのだが, モデルによっては十分に片方のパラメーターの探索が行われないという自体に陥ってしまう. それくらいならば, しっかりと一つ一つのモデルに対してパラメーターの探索をさせて, その上でモデルのgoodness of fitに関する指標で比較した方が良いと感じた.
の文献のCh.9のEM algorithmの実装が今回のscikit-learnのGMMに該当して, Ch.10.2の変分法の実装が, scikit-learnのVBGMMの "weight_concentration_prior_type"を"dirichlet_distribution"にしたものに該当する. 参照のこと.
参考文献
[1]Gaussian Mixture Model Selection, https://scikit-learn.org/stable/auto_examples/mixture/plot_gmm_selection.html#sphx-glr-auto-examples-mixture-plot-gmm-selection-py
[2] Christopher M. Bishop, Pattern Recognition and Machine Learning
[3] pythonで混合正規分布実装, https://qiita.com/ta-ka/items/3e8b127620ac92a32864
[4] GMM covariances, https://scikit-learn.org/stable/auto_examples/mixture/plot_gmm_covariances.html#sphx-glr-auto-examples-mixture-plot-gmm-covariances-py
[5] sklearn.mixture.GaussianMixture , https://scikit-learn.org/stable/modules/generated/sklearn.mixture.GaussianMixture.html#sklearn.mixture.GaussianMixture
[6] Choosing the right estimator, https://scikit-learn.org/stable/tutorial/machine_learning_map/index.html
[7] 2.1. Gaussian mixture models, https://scikit-learn.org/stable/modules/mixture.html
- PRML第9章 混合ガウス分布 Python実装, https://qiita.com/ctgk/items/22ce61fc0ffbc12c64d1
- VBGMM(クラスタ分析)【Pythonとscikit-learnで機械学習:第13回】, http://neuro-educator.com/ml13/
- 2.3. Clustering, https://scikit-learn.org/stable/modules/clustering.html


コメント